I originally didn’t want to write another blog post about Advent of Code, especially not consecutive ones. However, the solution to the second part of the fifth day was so interesting that I couldn’t resist. The puzzle is about mapping intervals to one another.

So let’s get started, shall we?

The puzzle

To understand the puzzle, let’s have a look at the example input from the puzzle:

seeds: 79 14 55 13

seed-to-soil map:
50 98 2
52 50 48

soil-to-fertilizer map:
0 15 37
37 52 2
39 0 15

fertilizer-to-water map:
49 53 8
0 11 42
42 0 7
57 7 4

water-to-light map:
88 18 7
18 25 70

light-to-temperature map:
45 77 23
81 45 19
68 64 13

temperature-to-humidity map:
0 69 1
1 0 69

humidity-to-location map:
60 56 37
56 93 4

Our input is a list of maps (for example the seed-to-soil map). Each line should be read as destination source length¹. So the source is a seed, the destination is a soil. In other words, in the example input, we’re given two intervals:

• $[50, 50 + 48)$ which maps to $[52, 52 + 48)$, and
• $[98, 98 + 2)$ which maps to $[50, 50 + 2)$.

If we have no specific mapping defined, a number just stays the same.

In the first line we’re also given ranges of seed IDs (a start and a length). In the example input, we need to look at $[79, 79 + 14]$ and $[55, 55 + 13]$.

We’re now supposed to use each map in succession to go from our seed IDs to locations. The goal of the puzzle is to find the smallest location number for all given seeds.

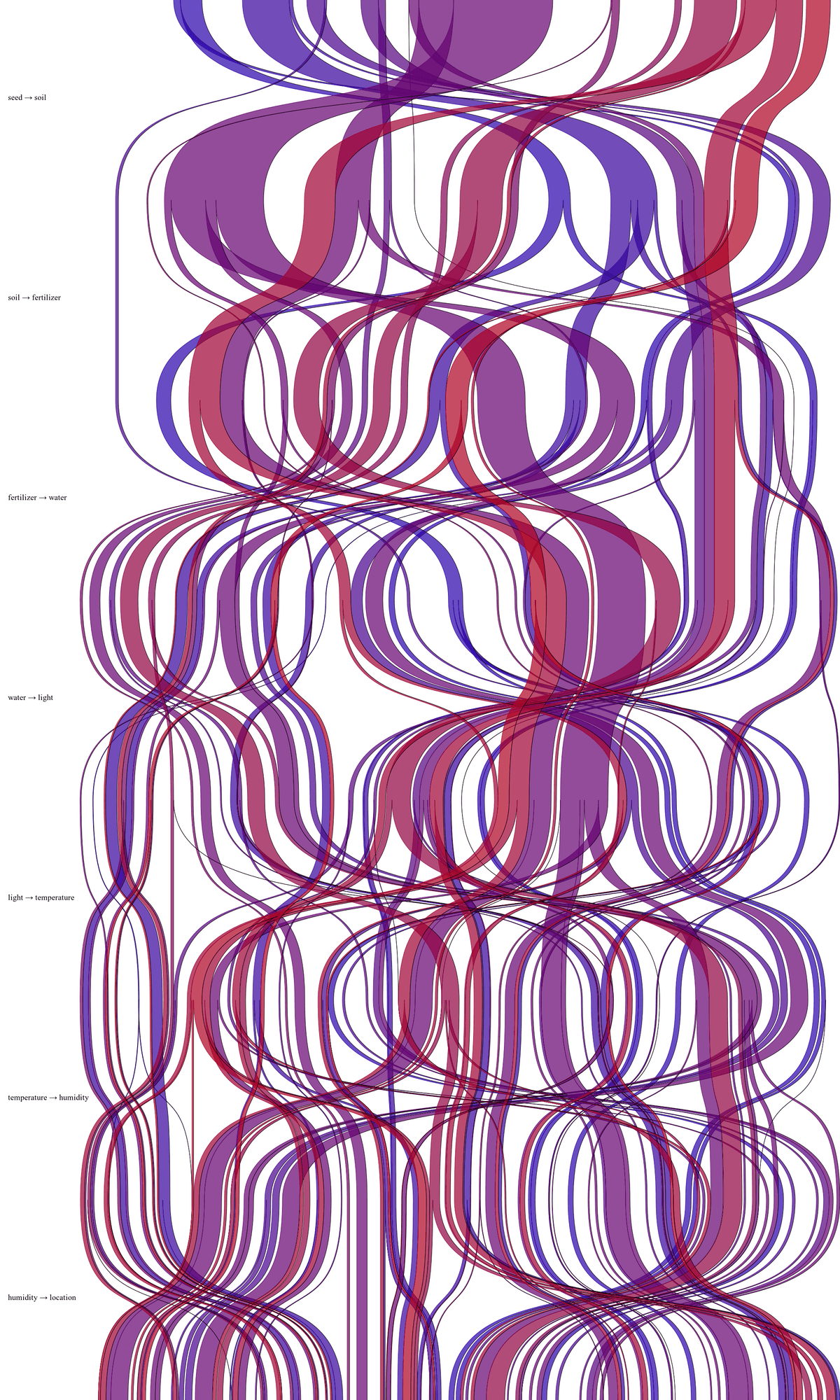
Below you can find a cool visualization of the problem by reddit user /u/NullPointerExcept10n². It shows how ranges of seeds map to different soils, humidities, …, and locations.

Let’s look at this mathematically

We can understand each of these maps as a function $\mathbb{N}_0 \to \mathbb{N}_0$ like this:

$$\text{soil}(x) = \begin{cases} x + 2 \text{ if } x \in [50, 98), \\ x - 48 \text{ if } x \in [98, 100), \\ x \text{ otherwise.} \end{cases}$$

Thus, our goal is — for a given set of seeds $S$ — to find³

$$\min_{x \in S} \left[ (\text{soil} \circ \text{fertilizer} \circ \dots \circ \text{humidity} \circ \text{location})(x) \right].$$

We can make some immediate observations:

1. We can express our set of seeds as a union of intervals. For any set of seeds $S$ we can construct

   $$S = \bigcup_i S_i,$$

   where $S_i$ is a family of intervals and $\forall i, j: S_i \cap S_j = \emptyset$ (the intervals are pairwise disjunct).

2. We can rewrite our functions to make all intervals explicit. We can also change $f$ to be a bit more explicit. Instead of just saying ”$x$ otherwise”, we can precisely specify under which circumstances $x$ maps to itself. For example

   $$\text{soil}(x) = \begin{cases} x \text{ if } x \in [0, 50), \\ x + 2\text{ if } x \in [50, 98), \\ x - 48 \text{ if } x \in [98, 100), \\ x \text{ if } x \in [100, \infty). \end{cases}$$

   We can clearly see that $\text{soil}$ is made up of four different mapping intervals. Let’s call these intervals $I_{f, i}$, where $f$ is the corresponding function and $i \in \mathbb{N}$ their index. We know (because $f$ is a function) that these intervals are pairwise disjunct as well.

   Let’s keep the intervals well-ordered: if $[b, c) = I_{f, i}$, then $[a, b) = I_{f, i - 1}$ and $[c, d) = I_{f, i + 1}$⁴.

3. For any given interval $I_{f, i}$, the value of $f$ increases monotonically. For example, let’s look at the interval $[50, 98)$. We can see that $\text{soil}(50) = 102$ and $\text{soil}(97) = 149$.

   This has severe implications. Because we know that within intervals the value is monotonically increasing, we don’t have to look at all values in an interval, we can “short circuit”:

   $$\exists i: [a, b] \subseteq I_{f, i} \implies \min_{x \in [a, b]} f(x) = f(a).$$

With this in hand, we can start asking the big questions:

What does $f \circ g$ actually look like?

We already discussed that we can express our functions $f$ and $g$ as families of intervals $I_{f, i}$ and $I_{g, i}$. Thus, asking “what does $f \circ g$ look like?” is really asking for $I_{f \circ g, i}$.

Let’s pick any $i$. We can now look at a new set $T_i = g(I_{f, i})$. What does $T_i$ look like? In the general case

$$T_i = \bigcup_j J_j, \text{ with } J_j \subseteq I_{g, k}.$$

In plain English: $T_i$ consists of a subsets of a subset of $g$’s intervals.

Intuitively, this makes sense. We can also see that

$$I_{f \circ g} = \bigcup_i T_i.$$

So how do we actually find the $T_i$?

Implementing the idea

Maybe now is the time to move away from mathematical notation and actually get started coding.

Step 1: Fixing the intervals

We start with a list of three-tuples for each map (start, length, destination). We want to now add the missing intervals like in the “Making intervals explicit” step above.

def make_intervals_explicit(
    mapping: list[tuple[int, int, int]]
) -> list[tuple[int, int]]:
    ret = []

    for i, (start, length, destination) in enumerate(mapping):
        ret.append((start, destination))

        # If the next interval is not directly adjacent, we have to insert a new one
        # Do this for the last interval in any case
        if (i != len(mapping) - 1 and mapping[i + 1][0] != start + length) or (
            i == len(mapping) - 1
        ):
            ret.append((start + length, start + length))

    # Add a starting interval if mapping didn't start with 0
    if ret[0][0] != 0:
        ret.insert(0, (0, 0))

    return merge_intervals(ret)

This function will for a given function (mapping) $f$ return $I_f$. Another way to think of the output is a list of tuples $(x_i, f(x_i))$.

Note that the function also merges intervals if possible:

def merge_intervals(l: list[tuple[int, int]]) -> list[tuple[int, int]]:
    # Someone who's better in python than me tell me if we actually need
    # this copy
    ret = l 

    i = 1
    # Merge intervals if possible
    while i < len(ret) - 1:
        start, start_value = ret[i]
        end, end_value = ret[i + 1]

        if start_value + (end - start) == end_value:
            del ret[i + 1]
        i += 1
    return ret

Step 2: Calculating all intersecting intervals

As a next step, we can get started calculating for an interval $[a, b]$ to find all intervals $I_{f, i}$ it intersects. This is the step where we calculate $T_i$.

def get_intersected_intervals(
    start: int, end: int | None, mapping: list[tuple[int, int]]
) -> list[tuple[int, int]]:
    ret = [
        value
        for value in mapping
        if start <= value[0] and (end is None or end >= value[0])
    ]

    # We need to fill the interval from the left
    if len(ret) == 0 or ret[0][0] > start:
        start_index = bisect.bisect_left(mapping, (start,)) - 1
        x, f_x = mapping[start_index]

        ret.insert(0, (start, f_x + (start - x)))

    return ret

First, we get all intervals that start within start and end ($J_i$ earlier). This covers our entire interval $T_i$ except for the first part: For that we need to take the previous interval (the one that starts before start) and clamp it so it starts at start. We use Python’s bisect module to find the intervals that start before start.

Step 3: Calculating $f \circ g$

We can now get started calculating the function composition. We discussed that $T_i = \bigcup_i J_i$. We also know that we can get $J_i$ from get_intersected_intervals().

def compose(
    f: list[tuple[int, int]], g: list[tuple[int, int]]
) -> list[tuple[int, int]]:
    ret = []

    for (x_start, f_start), (x_end, _) in zip(f, f[1:]):
        length = x_end - x_start

        ret.extend(
            [
                (start - (f_start - x_start), projection)
                for start, projection in get_intersected_intervals(
                    f_start, f_start + length, g
                )
            ]
        )

    f_start = f[-1][1]
    ret.extend(
        [
            (start, projection)
            for start, projection in get_intersected_intervals(f_start, None, g)
        ]
    )

    return ret

We use Python’s zip method⁵ to get our intervals $I_{i, f}$. As a last step, we add the last interval back.

Step 4: Lookup

To solve the puzzle, we finally need a function lookup that actually uses one of these maps to find the value. The input to this function are the $S_i$ from earlier. Here’s the code:

def lookup(start: int, end: int, f: list[tuple[int, int]]):
    values = [mapping for _, mapping in get_intersected_intervals(start, end, f)]

    return min(values)

Here we use the short-circuiting we discussed earlier: get_intersected_intervals will return the starting points for each interval. Because the intervals are strictly monotonic, we never want to evaluate beyond their starting point. Hence, it is sufficient to just take the minimum of each starting point’s value.

Step 5: Profit!

With all this set-up, we can finally calculate our entire function composition.

First, we set up our maps:

seed_to_soil_map = make_intervals_explicit(
    parse_map(_seed_to_soil.splitlines()[1:])
)
soil_to_fertilizer_map = make_intervals_explicit(
    parse_map(_soil_to_fertilizer.splitlines()[1:])
)
fertilizer_to_water_map = make_intervals_explicit(
    parse_map(_fertilizer_to_water.splitlines()[1:])
)
water_to_light_map = make_intervals_explicit(
    parse_map(_water_to_light.splitlines()[1:])
)
light_to_temp_map = make_intervals_explicit(
    parse_map(_light_to_temp.splitlines()[1:])
)
temp_to_humidity_map = make_intervals_explicit(
    parse_map(_temp_to_humidity.splitlines()[1:])
)
humidity_to_location_map = make_intervals_explicit(
    parse_map(_humidity_to_location.splitlines()[1:])
)

We then combine them into one complete map:

total_map = reduce(compose, [
    seed_to_soil_map,
    soil_to_fertilizer_map,
    fertilizer_to_water_map,
    water_to_light_map,
    light_to_temp_map,
    temp_to_humidity_map,
    humidity_to_location_map,
])

Because we’re fancy, we use functool’s reduce instead of writing it out. reduce applies compose cumulatively from left to right to the items of sequence.

Finally, the solution of the puzzle (find the smallest location for ranges of seeds) can be found by

values_part2 = [
    lookup(start, start + length, total_map)
    for start, length in zip(seeds[::2], seeds[1::2])
]
print(f"Part 2: {min(values_part2)}")

Footnotes

1. Not my fault they decided on doing it this way. Each time I read the input I get confused as well. ↩

2. Thanks again for letting me use it in my blog! ↩

3. ”$\circ$” denotes function composition (e.g. $f \circ g$ means $f(g(x))$). ↩

4. This is a bit imprecise, because if $i = 0$ or $i = |I_f|$, we apply 0 or $\infty$ as the borders respectively, but the idea is still the same. ↩

5. This code uses some pythonic pattern, which is to call zip() with the same list. The idea is to generate pairs of adjacent items from the list. This StackOverflow Answer has more information. ↩